Industrial Problem: Hoses Production Optimization (HoP)

edited by David Huber, AntOptima

Contents

Introduction Problem definition Objective function Metaheuristics User interface

Introduction

The problem under investigation is about the optimization of hoses production (HoP for short) in an important Italian factory for which AntOptima made a preliminary feasibility study. The HoP is a scheduling problem that is defined by a set of real orders to be executed by a group of multi-purpose machines. Typically, for each input data there are 300 orders consisting of about 800'000 meters of hoses. Each input data specifies the production of about one month. For each order there are constraints and requirements that must be satisfied (like deadlines, raw materials demand, precedence constraints, priorities, etc.). The production must be scheduled on 35 machines with different characteristics and requirements. The goal is to organize the production without violating the "main" constraints and minimizing an objective function that takes into consideration several aspects such as the penalties of violating constraints, the customers' priorities, and so on.

Problem definition

In the HoP problem we have a set of customers orders. Each order is defined by the type of hose to be produced, by the quantity, by a deadline time and by a release time (the release and the deadline define the production time window).
Fig. 1: a braiding machine The set of orders is partitioned into a set of n Jobs J = {J₁,...,J_n} according to the hose type (from a set T = {T₁,...,T_j} of types), order deadline-release and machine production slot (the latter is the discrete minimal amount of hoses that a machine can produce). Moreover, we have a set of m machines M = {M₁,...,M_m} that are used for the hoses production (a machine example is shown in fig. 1). Each job of type T_j must be processed, without interruptions, by a machine k out of a set M_j of given machines from M. The subset M_j is defined according to technological constraints.

Other constraints of the problems are listed below.

1. (MACHINE-BREAK-TIME) Machines cannot work always, machine-break-time (for maintenance, breakage, strike, etc.); A job cannot be scheduled on a machine during its machine-break-time.
2. (SLOT) For each hose type t and each machine m, it is defined a minimal discrete amount of production that is called slot s (the amount of hose type t that can be produced by machine m is a multiple of s).
3. (PROCESSING TIME) The processing time of job J_i on machine k is a given positive value p_ik that depends on the speed of the machine, on the hose type and on the quantity to be produced.
4. (TIME-WINDOW) Jobs have starting and end time windows. A job J_i should be processed during the time window [release_i, deadline_i]. Violations of the time window are allowed, with penalties, only for the completion time.
5. (SET-UP) Before processing a job on a machine, the chosen machine must be equipped, the time to make the latter is called setup time. Job J_i on machine k requires a setup time which depends on its type, on the type of its machine predecessor and on the machine itself.
6. (FROZEN JOBS) A job J_i can be frozen on a given machine k at a specific time s_i.

Objective function

The goal is to choose, for each jobs J_i, a machine k of M_i and a starting time s_i so that the weighted combination of:

• maximum completion time (makespan),
• sum of all jobs tardiness,
• sum of all setup times and
• difference of machine completion times

Metaheuristics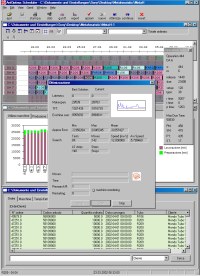

The environment implements the following search algorithms:

• Ant Colony Optimization
• Evolutionary Computation
• Iterated Local Search
• Simulated Annealing
• Tabu Search

User interface

We implemented a Graphical environment for the management of schedules. The user can build, search and edit solutions interactively through a simple yet powerful interface.

Data is loaded from a local or remote database. Many constraints, like machine-break-times, frozen states, time windows, ecc. can be changed at runtime. This allows operators to simulate different scenarios and evaluate warehouses occupations.